Un rincón para R - Modelos de variable dependiente binaria

A continuación abordaremos la estimación de un modelo de regresión lineal múltiple con variable dependiente binaria. Si bien, en mi web docente podéis encontrar este análisis, en este caso realizaremos el mismo usando funciones creadas especificamente para ello.

Más concretamente, se tienen las siguientes funciones:

ODDs: función que calcula el odd asociado a una observación concreta. Los argumentos de entrada son los coeficientes estimados del modelo logit/probit, los valores de la observación para la que se calcula el odd y un valor binario que indica si el modelo con el que se trabaja es un logit (valor por defecto) o un probit. Como salida proporciona el valor de z, la probabilidad de éxito, p, y el valor del odd.
ODD_RATIO: función que calcula el odd-ratio asociado a una variable independiente. Los argumentos de entrada son los coeficientes estimados del modelo logit/probit, los valores de las observaciones que determinan el odd-ratio que se desea calcular y un valor binario que indica si el modelo con el que se trabaja es un logit (valor por defecto) o un probit. Para ello, la primera observación debe ser s unidades superior (por defecto s=1) a la segunda en la variable independiente para la que se quiere calcular el odd-ratio, al mismo tiempo que tienen exactamente los mismos valores en el resto de variables independientes. La salida es el valor del odd-ratio.
TASA_ACIERTOS: función que calcula el porcentaje de casos clasificados correctamente/erróneamente en los éxitos/fracasos. Los argumentos de entrada son el umbral que determina el éxito/fracaso, los valores estimados por el modelo logit/probit y los valores observados de la variable dependiente. Como salida da la proporción de aciertos cuando se produce un éxito, de errores cuando se produce un éxito, de aciertos cuando se produce un fracaso y de errores cuando se produce un fracaso.

Una vez descargado el archivo txt anterior con dichas funciones, lo cargamos mediante el código:

source("funciones.txt")

Los datos con los que vamos a trabajar se cargan (una vez descargados) mediante las órdenes:

datos = read.table("datos_RM.csv", header=T, sep=";")
head(datos) # vemos el nombre de cada una de las variables

  Resultado Llull Chacho Rudy Mirotic PR   PorcRT Q1 T1IR L
1         1     1      1    1       1 61 53.84615 25   21 0
2         1     0      1    0       1 79 48.43750 29   20 0
3         1     0      0    0       1 53 64.00000 26    6 1
4         1     1      0    1       1 63 43.54839 16   14 0
5         1     0      1    0       1 72 58.33333 26   18 1
6         1     1      0    0       1 58 59.45946 18    8 1

El objetivo en este caso es el de analizar qué factores influyen (y cómo lo hacen) en que el equipo de baloncesto del Real Madrid gane un partido (para más detalles, ver el siguiente trabajo). Para ello, se usan las siguientes variables:

Resultado: variable binaria que toma el valor 1 cuando el R. Madrid gana el partido y 0 en caso contrario (es la variable dependiente).
Llull, Chacho, Rudy y Mirotic: variables binarias que toman el valor 1 cuando el jugador en cuestión tiene una valoración superior a su media y 0 en caso contrario.
PR: puntos recibidos.
PorcRT: porcentaje de rebote total capturado.
Q1: puntos anotados en el primer cuarto.
T1IR: tiros libres intentados por el equipo rival.
L: variable binaria que toma el valor 1 cuando el R. Madrid juega como local y 0 en caso contrario.

Incorporamos los datos a R para referenciar cada variable por el nombre anterior:

attach(datos)

Regresión lineal múltiple: modelo lineal de probabilidad

Para simplicar el modelo inicial, vamos a trabajar con el siguiente: \[\mathbf{Resultado} = \beta_{1} + \beta_{2} \cdot \textbf{Mirotic} + \beta_{3} \cdot \mathbf{PorcRT} + \beta_{4} \cdot \mathbf{Q1} + \beta_{5} \cdot \mathbf{T1IR} + \beta_{6} \cdot \mathbf{L} + \mathbf{u}.\]

Su estimación por Mínimos Cuadrados Ordinarios (MCO) proporciona los siguientes resultados:

mlp = lm(Resultado~Mirotic+PorcRT+Q1+T1IR+L)
summary(mlp)


Call:
lm(formula = Resultado ~ Mirotic + PorcRT + Q1 + T1IR + L)

Residuals:
     Min       1Q   Median       3Q      Max 
-0.80465 -0.09943  0.10259  0.22222  0.38260 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)   
(Intercept)  0.211142   0.392541   0.538  0.59229   
Mirotic      0.129142   0.075635   1.707  0.09199 . 
PorcRT       0.008727   0.007105   1.228  0.22331   
Q1           0.016589   0.007475   2.219  0.02957 * 
T1IR        -0.014983   0.005383  -2.783  0.00685 **
L            0.038960   0.077497   0.503  0.61667   
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.3144 on 73 degrees of freedom
Multiple R-squared:  0.2909,    Adjusted R-squared:  0.2423 
F-statistic: 5.989 on 5 and 73 DF,  p-value: 0.0001071

Se observa que, al 5% de significación, el modelo es conjuntamente válido (p-valor a sociado al contraste de significación conjunta igual a 0.0001071 y, por tanto, menor que 0.05). Al mismo tiempo, el coeficiente de determinación es bajo, 29.09%, lo cual es esperable ya que en esencia se tiene una relación no lineal.

Finalmente, de las variables independientes consideradas, sólo dos tienen el coeficiente asociado significativamente distinto de cero al 5% de significación. Se puede concluir entonces que:

Cuando se anota un punto más en el primer cuarto, la probabilidad de ganar el partido aumenta en un 1.65%.
Cuando el equipo rival intenta un tiro libre más, la probabilidad de ganar el partido disminuye un 1.49%.

Representando los valores estimados a partir del modelo ajustado, se puede observar que se obtienen estimaciones superiores a 1 (línea roja):

est.mlp = mlp$fitted.values
plot(est.mlp, xlab="Partido", ylab="Estimación de RESULTADO", col="blue",lwd=2)
abline(a=1,b=0,col="red",lwd=2) # línea y=1
abline(a=0,b=0,col="red",lwd=2) # línea y=0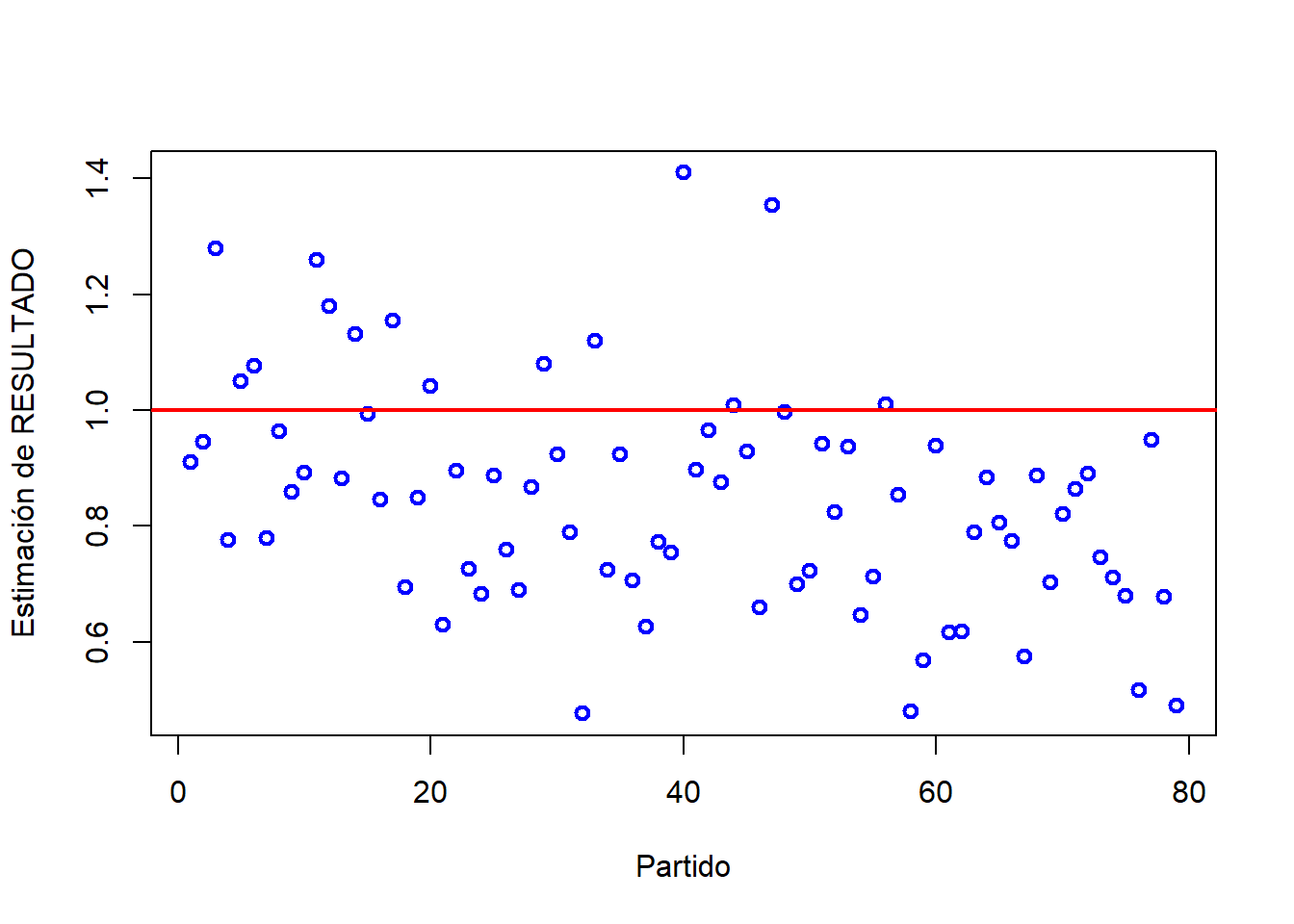

Puesto que en este modelo las estimaciones se interpretan como probabilidades (concretamente, la probabilidad de ganar un partido), esta situación es difícil de justificar.

Para solventar esta pega (y otras conocidas que pueden aparecer al estimar por MCO este tipo de modelos con variable dependiente discreta), a continuación se aborda el uso de modelos logit y probit.

Logit

Para estimar el modelo planteado según un enfoque logit, usaremos el comando glm como sigue:

logit = glm(Resultado~Mirotic+PorcRT+Q1+T1IR+L, family=binomial("logit"))
summary(logit)


Call:
glm(formula = Resultado ~ Mirotic + PorcRT + Q1 + T1IR + L, family = binomial("logit"))

Deviance Residuals: 
     Min        1Q    Median        3Q       Max  
-2.86952   0.00142   0.03514   0.17169   1.18379  

Coefficients:
            Estimate Std. Error z value Pr(>|z|)   
(Intercept) -17.5478     8.1676  -2.148  0.03168 * 
Mirotic       3.9430     1.8692   2.109  0.03491 * 
PorcRT        0.3181     0.1454   2.187  0.02874 * 
Q1            0.4531     0.1834   2.471  0.01347 * 
T1IR         -0.3374     0.1279  -2.638  0.00835 **
L             2.4085     1.4629   1.646  0.09969 . 
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(Dispersion parameter for binomial family taken to be 1)

    Null deviance: 67.306  on 78  degrees of freedom
Residual deviance: 27.483  on 73  degrees of freedom
AIC: 39.483

Number of Fisher Scoring iterations: 8

Atendiendo a los resultados obtenidos se puede afirmar, al 5% de significación, que:

Las variables Mirotic, PorcRT y Q1 tienen asociado un coeficiente positivo significativamente distinto de cero, por tanto, incrementos en estas variables suponen un aumento en la probabilidad de ganar un partido.
La variable T1IR tiene asociado un coeficiente negativo significativamente distinto de cero, por tanto, incrementos en esta variable supone una disminución en la probabilidad de ganar un partido.

¿De cuánto es el aumento o la disminución? Para ello hay que recurrir al odd-ratio asociado a cada variable, ya que del coeficiente estimado sólo se puede interpretar su signo. En el caso del logit, esta cantidad se puede calcular directamente a partir del coeficiente estimado calculando su exponencial:

exp(logit$coefficients[-1]) # quito el coeficiente estimado de la constante

   Mirotic     PorcRT         Q1       T1IR          L 
51.5727677  1.3744799  1.5732301  0.7136264 11.1167443

1/0.7136264

[1] 1.401293

A partir de los resultados obtenidos, se podría afirmar que:

Cuando Mirotic tiene una valoración superior a su media es 51.572 veces más probable que se gane el partido frente a que no se haga que cuando no la tiene, suponiendo que el resto de variables permanecen constantes.
Cuando se captura un 1% de rebote total es 1.374 veces más probable que se gane el partido frente a que no se haga que cuando no se captura, suponiendo que el resto de variables permanecen constantes.
Cuando se anota un punto más en el primer cuarto es 1.573 veces más probable que se gane el partido frente a que no se haga que cuando no se anota, suponiendo que el resto de variables permanecen constantes.
Cuando el rival intenta un tiro libre más es 1.401 veces menos probable que se gane el partido frente a que no se haga que cuando no se intenta, suponiendo que el resto de variables permanecen constantes.
Cuando se juega como local es 11.116 veces más probable que se gane el partido frente a que no se haga que cuando no se juega como visitante, suponiendo que el resto de variables permanecen constantes.

Usando las funciones comentadas al principio del post, concretamente ODD_RATIO, el odd-ratio asociado a la variable Mirotic se podría calcular como sigue:

ind1 = c(1, 1, 50, 20, 20, 1) # partido en el que Mirotic supera su valoración media, se captura el 50% del rebote total, se anotan 20 puntos en el primer cuarto, el rival intenta 20 tiros libres y se juega como local
ind2 = c(1, 0, 50, 20, 20, 1) # partido en el que Mirotic no supera su valoración media, se captura el 50% del rebote total, se anotan 20 puntos en el primer cuarto, el rival intenta 20 tiros libres y se juega como local
ODD_RATIO(logit$coefficients, ind1, ind2)

[1] 51.57277

#
ind3 = c(1, 1, 70, 26, 15, 0) # partido en el que Mirotic supera su valoración media, se captura el 70% del rebote total, se anotan 26 puntos en el primer cuarto, el rival intenta 15 tiros libres y se juega como visitante
ind4 = c(1, 0, 70, 26, 15, 0) # partido en el que Mirotic no supera su valoración media, se captura el 70% del rebote total, se anotan 26 puntos en el primer cuarto, el rival intenta 15 tiros libres y se juega como visitante
ODD_RATIO(logit$coefficients, ind3, ind4)

[1] 51.57277

Adviértase que en ambos casos se han usado dos observaciones en las que la única diferencia radica en la variable Mirotic.

También se podría haber calculado los odd-ratio paso a paso usando la función ODDs. Por ejemplo, para la variable PorcRT:

ind5 = c(1, 0, 50, 20, 25, 0) # partido en el que Mirotic no supera su valoración media, se captura el 50% del rebote total, se anotan 20 puntos en el primer cuarto, el rival intenta 25 tiros libres y se juega como visitante
ODDs(logit$coefficients, ind5)

          z         p       odd
1 -1.016285 0.2657516 0.3619369

ind6 = c(1, 0, 49, 20, 25, 0) # partido en el que Mirotic no supera su valoración media, se captura el 49% del rebote total, se anotan 20 puntos en el primer cuarto, el rival intenta 25 tiros libres y se juega como visitante
ODDs(logit$coefficients, ind6)

          z         p       odd
1 -1.334361 0.2084389 0.2633264

#
0.3619369/0.2633264

[1] 1.37448

Además, se puede observar, por ejemplo, que un partido en el que Mirotic no supera su valoración media, se captura el 50% del rebote total, se anotan 20 puntos en el primer cuarto, el rival intenta 25 tiros libres y se juega como visitante es 2.762913 veces menos probable que se consiga la victoria frente a que no se consiga.

2.762913

[1] 2.762913

Los odds también se podrían calcular directamente calculando la exponencial de z:

exp(-1.016285)

[1] 0.361937

exp(-1.334361)

[1] 0.2633264

Finalmente, la bondad del ajuste se puede obtener a partir de la función TASA_ACIERTOS para calcular la tabla de clasificación:

TASA_ACIERTOS(mean(Resultado), fitted.values(logit), Resultado)

  exito_aciertos_A exito_errores_B fracaso_errores_C fracaso_aciertos_D
1         69.62025        1.265823          15.18987           13.92405
  tasa_aciertos
1       83.5443

En este caso, en el que se ha usado la proporción de éxitos (partidos ganados) existentes en la variable dependiente como punto de corte que clasifica los valores estimados (probabilidades) como un éxito/fracaso, se tiene que:

Se clasifica correctamente el 69.62% y erróneamente el 1.26% de los partidos en los que se gana.
Se clasifica correctamente el 13.92% y erróneamente el 15.18% de los partidos en los que se pierde.
Se clasifica correctamente el 83.54% (69.62% + 13.92%) de los partidos.

Probit

Para estimar usando un modelo probit se usará el siguiente código:

probit = glm(Resultado~Mirotic+PorcRT+Q1+T1IR+L, family=binomial("probit"))
summary(probit)


Call:
glm(formula = Resultado ~ Mirotic + PorcRT + Q1 + T1IR + L, family = binomial("probit"))

Deviance Residuals: 
     Min        1Q    Median        3Q       Max  
-2.57648   0.00000   0.01167   0.20474   1.28761  

Coefficients:
            Estimate Std. Error z value Pr(>|z|)   
(Intercept) -9.21729    4.02478  -2.290  0.02201 * 
Mirotic      1.87380    0.85935   2.180  0.02922 * 
PorcRT       0.16044    0.07066   2.271  0.02317 * 
Q1           0.25028    0.08949   2.797  0.00516 **
T1IR        -0.17087    0.06024  -2.837  0.00456 **
L            1.24450    0.76856   1.619  0.10539   
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(Dispersion parameter for binomial family taken to be 1)

    Null deviance: 67.306  on 78  degrees of freedom
Residual deviance: 28.100  on 73  degrees of freedom
AIC: 40.1

Number of Fisher Scoring iterations: 10

Se puede observar que el código es totalmente análogo al anterior simplemente cambiando la familia logit por la probit.

Atendiendo a la significación individual, se obtienen los mismos coeficientes significativamente distintos de cero que en el caso anterior. Puesto que se tienen también los mismos signos estimados, las implicaciones que tienen sobre la probabilidad de ganar un partido son las mismas que en el modelo logit.

Sin embargo, al igual que antes, sólo es posible interpretar el signo, no la magnitud. Para ello habría que recurrir al odd y odd-ratio.

Por ejemplo, para un partido en el que Mirotic no supera su valoración media, se captura el 50% del rebote total, se anotan 20 puntos en el primer cuarto, el rival intenta 25 tiros libres y se juega como local, la probabilidad de victoria es del 78.31%, siendo 3.611 veces más probable que se gane frente a que se pierda:

ind6 = c(1, 0, 50, 20, 25, 1) 
ODDs(probit$coefficients, ind6, logit=0)

          z         p      odd
1 0.7828876 0.7831534 3.611556

Mientras que para un partido en el que Mirotic no supera su valoración media, se captura el 50% del rebote total, se anotan 20 puntos en el primer cuarto, el rival intenta 25 tiros libres y se juega como visitante, la probabilidad de victoria es del 32.21%, siendo 2.103 veces menos probable que se gane frente a que se pierda:

ind7 = c(1, 0, 50, 20, 25, 0) 
ODDs(probit$coefficients, ind7, logit=0)

           z        p     odd
1 -0.4616088 0.322181 0.47532

1/0.47532

[1] 2.103846

Mediante el cociente de ambos odds, se obtiene que cuando se juega como local es 7.598156 veces más probable que se gane frente a que se pierda que cuando se juega como visitante, suponiendo que el resto de variables permanece constante:

3.611556/0.47532

[1] 7.598157

ODD_RATIO(probit$coefficients, ind6, ind7, logit=0)

[1] 7.598156

Finalmente, en este caso se clasifican correctamente el 81.01% de los partidos:

TASA_ACIERTOS(mean(Resultado), fitted.values(probit), Resultado)

  exito_aciertos_A exito_errores_B fracaso_errores_C fracaso_aciertos_D
1         67.08861        1.265823          17.72152           13.92405
  tasa_aciertos
1      81.01266

Selección de modelos

En los resultados obtenidos se observa que el valor del criterio de Akaike (AIC) en el modelo logit es igual a 39.483, mientras que en el modelo probit es igual a 40.1.

Al mismo tiempo, el primer modelo clasifica correctamente el 83.54% de los casos, mientras que el segundo al 81.01%.

Finalmente, la log-verosimilitud del modelo logit es igual a -13.742, mientras que la del probit es igual a -14.05:

library(memisc) # install.packages("memisc")
mtable(logit, probit)


Calls:
logit: glm(formula = Resultado ~ Mirotic + PorcRT + Q1 + T1IR + L, family = binomial("logit"))
probit: glm(formula = Resultado ~ Mirotic + PorcRT + Q1 + T1IR + L, family = binomial("probit"))

========================================
                    logit     probit    
----------------------------------------
  (Intercept)     -17.548*    -9.217*   
                   (8.168)    (4.025)   
  Mirotic           3.943*     1.874*   
                   (1.869)    (0.859)   
  PorcRT            0.318*     0.160*   
                   (0.145)    (0.071)   
  Q1                0.453*     0.250**  
                   (0.183)    (0.089)   
  T1IR             -0.337**   -0.171**  
                   (0.128)    (0.060)   
  L                 2.408      1.244    
                   (1.463)    (0.769)   
----------------------------------------
  Log-likelihood  -13.742    -14.050    
  N                79         79        
========================================
  Significance: *** = p < 0.001;   
                ** = p < 0.01;   
                * = p < 0.05

Por tanto, todo los datos anteriores indican que el modelo logit es preferible al probit.