Multicolinealidad

Una vez que hemos visto situaciones en las que el análisis del modelo de regresión lineal múltiple se puede ver afectado tanto desde el punto de vista estadístico (se ve afectada la inferencia individual), como numérico (obtención de coeficientes estimados inesperados), se hace necesario disponer de herramientas que permitan determinar si el grado de multicolinealidad existente es preocupante.

Más concretamente, a continuación trabajaremos con el coeficiente de variación, la matriz de correlaciones lineales simples y su determinante, el factor de inflación de la varianza, el número de condición y una representación gráfica de suma sencillez. Todas estas medidas están disponibles en las librerías multiColl y rvif. Para cargarlas hay que ejecutar el siguiente código:

library(multiColl) # install.packages(multiColl)
library(rvif) # install.packages(rvif)

Aunque antes de entrar en materia, es conveniente distinguir entre los dos tipos de multicolinealidad aproximada siguientes: esencial y no esencial. Así, dado el modelo de regresión lineal múltiple siguiente: \[\mathbf{y} = \beta_{1} + \beta_{2} \mathbf{X}_{2} + \beta_{3} \mathbf{X}_{3} + \cdots + \beta_{k} \mathbf{X}_{k} + \mathbf{u},\] se define la multicolinealidad aproximada esencial como la relación lineal aproximada existente entre las variables independientes excluido el término independiente; mientras que la no esencial hace referencia a la relación entre el término independiente y el resto de variables independientes.

Esta distinción es importante ya que no todas las herramientas que vamos a ver son capaces de detectarlas. Para ilustrarlo, usaremos los datos de Wissel y Wooldrigde con los que ya hemos trabajado:

wissel = read.table("https://rnoremlas.quarto.pub/un_rincon_para_r/posts/15_multicolinealidad/Wissel.txt", header=T, sep=";")
wooldridge = read.table("https://rnoremlas.quarto.pub/un_rincon_para_r/posts/15_multicolinealidad/Wooldridge.txt", header=T, sep=";")

Ahora bien, como la multicolinealidad aproximada es un problema que solo atañe a las variables independientes, nos quedaremos con estas y añadiremos la constante:

cte = rep(1, nrow(wissel))
wissel.X = cbind(cte, wissel[,-1])
#
cte = rep(1, nrow(wooldridge))
wooldridge.X = cbind(cte, wooldridge[,-3])

También usaremos los datos de Theil sobre el consumo textil:

data(theil) # datos disponibles en librería 'multiColl'
cte = rep(1, nrow(theil))
theil.X = cbind(cte, theil[,c(3,4)])

Echemos un vistazo a los datos con los que vamos a trabajar:

head(wissel.X)

  cte      C      I      Cr
1   1 4.7703 4.8786  808.23
2   1 4.7784 5.0510  798.03
3   1 4.9348 5.3620  806.12
4   1 5.0998 5.5585  865.65
5   1 5.2907 5.8425  997.30
6   1 5.4335 6.1523 1140.70

head(wooldridge.X)

  cte   r3   r6
1   1 2.77 3.02
2   1 2.97 3.43
3   1 4.00 4.32
4   1 4.60 4.68
5   1 4.16 4.33
6   1 3.07 3.50

head(theil.X)

     cte income relprice
[1,]   1   96.7    101.0
[2,]   1   98.1    100.1
[3,]   1  100.0    100.0
[4,]   1  104.9     90.6
[5,]   1  104.9     86.5
[6,]   1  109.5     89.7

Coeficiente de Variación

En el caso de que exista multicolinealidad aproximada no esencial se ha de verificar que una de las variables independientes (excluido el término independiente) ha de ser prácticamente constante. Por tanto, para detectarla se hace necesario usar una medida que sea capaz de detectar esta característica.

Usando el coeficiente de variación podemos determinar aquellas variables que son más homogéneas. Así, consideraremos que aquellas variables con un coeficiente de variación inferior a 0.1 son responsables de un problema de multicolinealidad no esencial:

  CVs(wissel.X)

[1] 0.1718940 0.2482804 0.3607848

  CVs(wooldridge.X)

[1] 0.4666176 0.4588348

  CVs(theil.X)

[1] 0.04993766 0.21441845

A partir de los resultados obtenidos, se tiene que la variable income de los datos de Theil está relacionada con el término independiente provocando un problema de multicolinealidad aproximada no esencial.

Matriz de correlaciones y su determinante

El coeficiente de correlación lineal simple permite detectar si la relación lineal entre dos variables cuantitativas es alta o baja. Al mismo tiempo, en el caso de ausencia de relaciones lineales, la matriz de correlaciones de las variables independiente coincidirá con la matriz identidad, cuyo determinante es uno. Así, cuanto más alejado esté este determinante de este valor, mayor serán las relaciones lineales existentes. Por simetría, se considerará que la multicolinealidad existente es preocupante cuando el determinante de la matriz de correlaciones sea próximo a cero.

Más concretamente, valores del coeficiente de correlación simple superiores a \(\sqrt{0.9}\) y determinantes de la matriz de correlaciones inferiores a 0.1, estarían indicando que las relaciones lineales existentes son altas.

Es importante destacar que puesto que el coeficiente de correlación no se puede calcular cuando una de las dos variables es constante, estas herramientas no son capaces de detectar la multicolinealdiad aproximada de tipo no esencial.

  RdetR(wissel.X)

$`Correlation matrix`
           C         I        Cr
C  1.0000000 0.9980960 0.9971663
I  0.9980960 1.0000000 0.9940621
Cr 0.9971663 0.9940621 1.0000000

$`Correlation matrix's determinant`
[1] 2.007699e-05

  RdetR(wooldridge.X)

$`Correlation matrix`
          r3        r6
r3 1.0000000 0.9965734
r6 0.9965734 1.0000000

$`Correlation matrix's determinant`
[1] 0.006841421

  RdetR(theil.X)

$`Correlation matrix`
            income  relprice
income   1.0000000 0.1788467
relprice 0.1788467 1.0000000

$`Correlation matrix's determinant`
[1] 0.9680139

Así, los resultados anteriores indican que:

• en el caso de los datos de Wissel, existe una alta relación lineal entre el consumo, los ingresos y el crédito pendiente,
• en el caso de los datos de Wooldridge, existe una alta relación lineal entre los tipos de interés entre tres y seis meses,
• en el caso de los datos de Theil, no existe una alta relación lineal entre los tipos de interés entre los ingresos y el índice de precios.

Factor de Inflación de la varianza

Considerando el coeficiente de determinación, que notaremos como \(R_{i}^{2}\), de la regresión (auxiliar) en la que la variable indpendiente i-ésima, con \(i=2,3,\dots,k\), se explica en función del resto de variables independientes: \[\mathbf{X}_{i} = \alpha_{1} + \alpha_{2} \mathbf{X}_{2} + \alpha_{3} \mathbf{X}_{3} + \cdots + \alpha_{i-1} \mathbf{X}_{i-1} + \alpha_{i+1} \mathbf{X}_{i+1} + \cdots + \alpha_{k} \mathbf{X}_{k} + \mathbf{v},\] se tiene que si éste es alto, se tendría que la relación lineal entre \(\mathbf{X}_{i}\) y el resto de variables independientes es alta. Y, esto es, ni más ni menos, que la definición de multicolinealdiad aproximada.

A partir de este coeficiente de determinación, se define el factor de inflación de la varianza como: \[FIV(i) = \frac{1}{1 - R^{2}_{i}}, \quad i=2,\dots,k.\]

Adviértase que se ha dejado fuera el término independiente ya que no es posible calcular el coeficiente de determinación de la regresión (auxiliar) en la que ésta aparece como dependiente. Por tanto, usando esta medida sólo es capaz de detectar la multicolinealdiad de tipo esencial.

En el momento que exista un FIV superior a 10, se considerará que la multicolinealidad aproximada (de tipo esencial) existente es preocupante.

Los siguientes resultados indican que la multicolinealdiad aproximada de tipo esencial existente en los dos primeros casos es preocupante; al contrario de lo que ocurre en el tercero:

  VIF(wissel.X)

       C        I       Cr 
589.7540 281.8862 189.4874 

  VIF(wooldridge.X)

      r3       r6 
146.1685 146.1685 

  VIF(theil.X)

  income relprice 
1.033043 1.033043 

Número de Condición

El número de condición se obtiene como: \[NC = \sqrt{\frac{\lambda_{max}}{\lambda_{min}}},\] donde \(\lambda_{max}\) y \(\lambda_{min}\) son los autovalores de la matriz \(\widetilde{\mathbf{X}}^{t}\widetilde{\mathbf{X}}\), siendo \(\widetilde{\mathbf{X}}\) la transformación en longitud unidad de la matriz \(\mathbf{X}\).

Valores del número de condición superiores a 20 indican multicolinealidad aproximada moderada y superiores a 30 preocupante.

Al mismo tiempo, puesto que se tiene en cuenta al término independiente, el número de condición es capaz de detectar tanto la multicolinealidad aproximada de tipo esencial como no esencial. Eso sí, si se ignora el término independiente, sólo se estaría trabajando con la del tipo esencial. Y su comparación con la anterior, permitiría cuantificar el papel del término independiente (multicolinealdiad aproximada no esencial).

Los siguientes resultados indican un papel relevante en el primer y tercer caso:

  CNs(wissel.X)

$`Condition Number without intercept`
[1] 105.0198

$`Condition Number with intercept`
[1] 332.3

$`Increase (in percentage)`
[1] 68.39609

  CNs(wooldridge.X)

$`Condition Number without intercept`
[1] 56.56906

$`Condition Number with intercept`
[1] 69.00941

$`Increase (in percentage)`
[1] 18.02704

  CNs(theil.X)

$`Condition Number without intercept`
[1] 9.576912

$`Condition Number with intercept`
[1] 48.95347

$`Increase (in percentage)`
[1] 80.43671

Más concretamente, en el tercer caso, se observa que si no se tiene en cuenta el término independiente (multicolinealidad aproximada esencial), el número de condición es inferior a 10; mientras que si se tiene en cuenta, pasa a ser superior a 30. Por tanto, el término indpendiente es el responsable de la multicolinealidad aproximada que detecta el número de condición.

Índice de Stewart y representación gráfica del coeficiente de variación frente al factor de inflación de la varianza

Todas las medidas anteriores están disponibles en el paquete multiColl, a continuación nos centraremos en la representación gráfica del coeficiente de variación frente al factor de inflación de la varianza, disponible en el paquete rvif.

En dicha representación gráfica, además de las medidas anteriores, se representan los umbrales dados para el coeficiente de variación y del factor de inflación de la varianza de forma que se tienen cuatro regiones que permiten:

• determinar si hay multicolinealdiad aproximada de tipo esencial o no esencial y
• qué variables la provocan.

Así, a partir de los siguientes resultados se puede establecer que:

• en el caso de los datos de Wissel, existe un problema de multicolinealidad aproximada de tipo esencial entre el consumo, los ingresos y el crédito pendiente,
• en el caso de los datos de Wooldridge, existe un problema de multicolinealidad aproximada de tipo esencial entre los tipos de interés entre tres y seis meses,
• en el caso de los datos de Theil, existe un problema de multicolinealidad aproximada de tipo no esencial entre los ingresos y el término independiente.

  RVIF(wissel.X)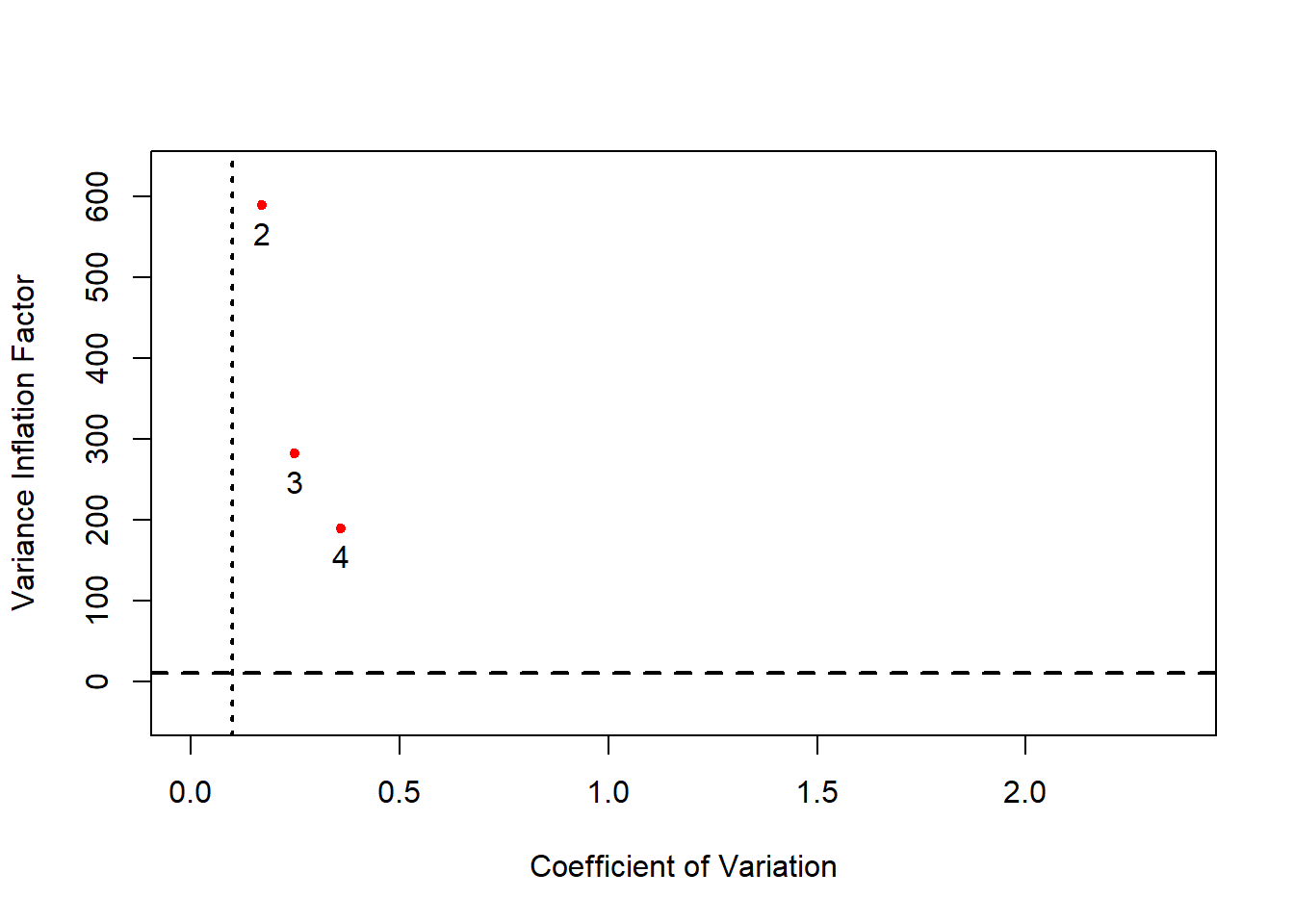

                RVIF       %
Intercept   3312.724 99.9698
Variable 2 20549.244 99.9951
Variable 3  4854.757 99.9794
Variable 4  1645.227 99.9392

  RVIF(wooldridge.X)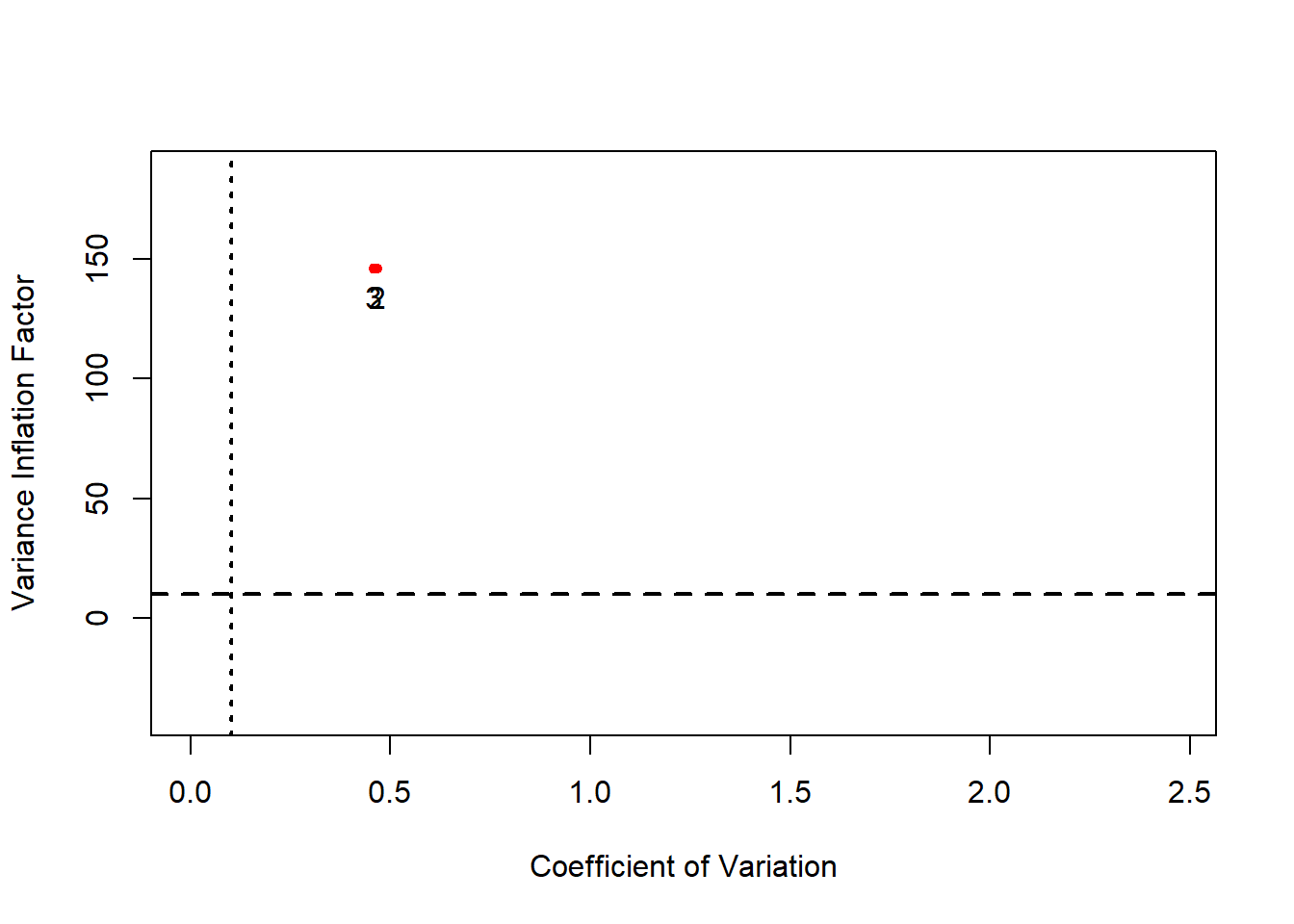

                 RVIF       %
Intercept    5.871871 82.9697
Variable 2 817.491287 99.8777
Variable 3 840.458579 99.8810

  RVIF(theil.X)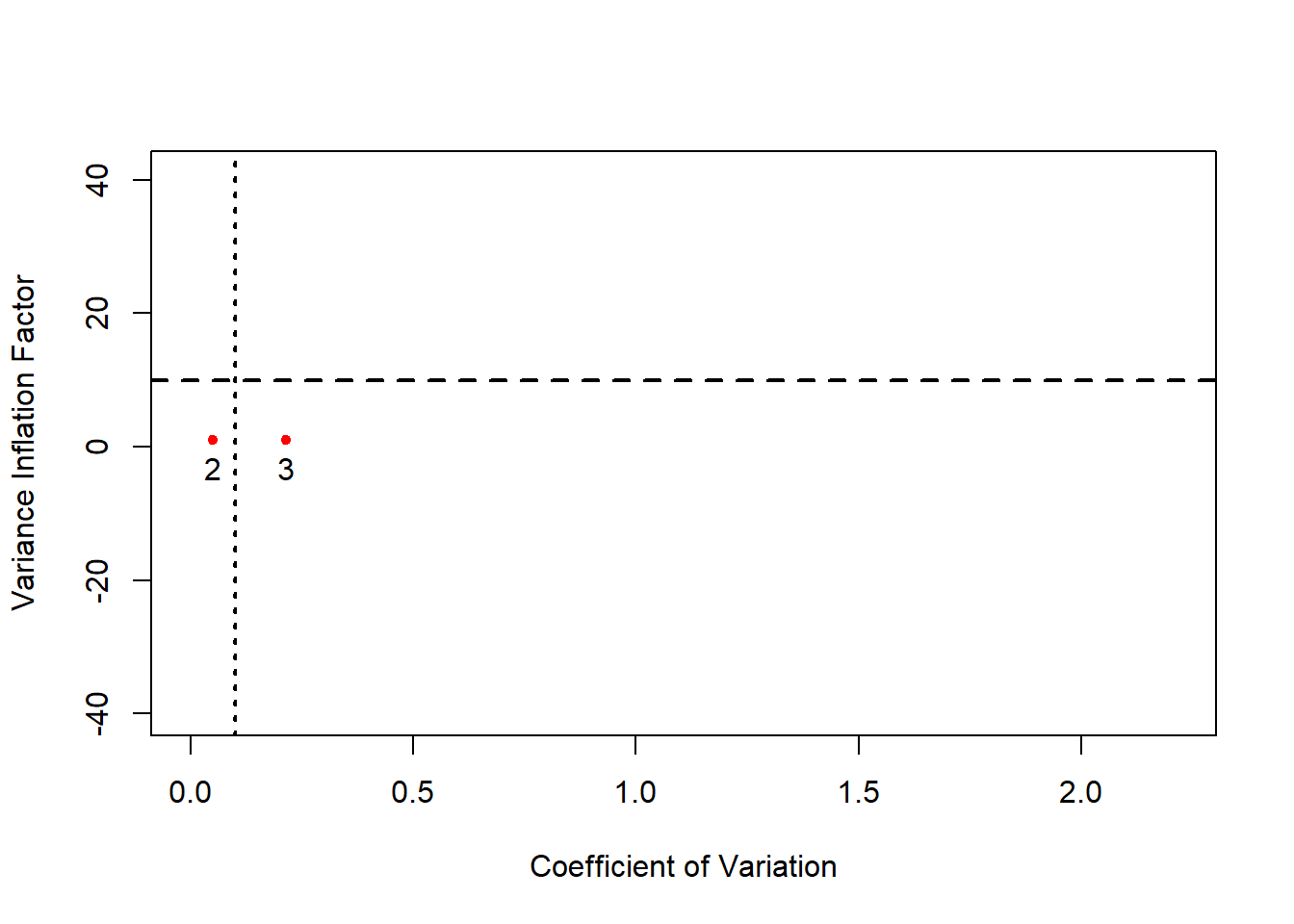

                RVIF       %
Intercept  403.20963 99.7520
Variable 2 415.28266 99.7592
Variable 3  23.50258 95.7451

Finalmente, los resultados numéricos obtenidos hacen referencia al índice de Stewart, otra medida habitualmente usada para detectar multicolinealdiad aproximada en un modelo de regresión lineal múltiple.