Multicolinealidad

Como hemos visto en el post dedicado a la estimación por Mínimos Cuadrados Ordinarios de un modelo de regresión lineal múltiple, una vez realizada ésta es obligatorio comprobar que las hipótesis de partida se verifican.

Así, es sabido que la existencia de relaciones lineales altas (multicolinealidad preocupante) entre las variables independientes puede afectar al análisis del modelo tanto desde el punto de vista estadístico como numérico. En este post, nos centraremos en el primero.

Entenderemos que el análisis estadístico se ha visto comprometido cuando la inferencia del modelo presente contradicciones difíciles de explicar. A continuación veremos dos ejemplos donde observaremos síntomas de que hay algo en el modelo que no funciona correctamente.

Contradicciones entre la inferencia individual y conjunta del modelo

Consideremos el conjunto de datos de Wissel sobre el análisis de las relaciones del consumo, ingresos y crédito pendiente sobre el crédito en Estados Unidos:

datos1 = read.table("Wissel.txt", header=T, sep=";")
names(datos1) # D = crédito, C = consumo, I = ingresos, Cr = crédito pendiente

[1] "D"  "C"  "I"  "Cr"

Al estimar el modelo \(\textbf{D} = \beta_{1} + \beta_{2} \textbf{C} + \beta_{3} \textbf{I} + \beta_{4} \textbf{Cr} + \textbf{u}\) por MCO se obtienen los siguientes resultados:

attach(datos1) # agrego las variables a la memoria para poder usarlas por su nombre
  modelo1 = lm(D~C+I+Cr)
  summary(modelo1)

Call:
lm(formula = D ~ C + I + Cr)

Residuals:
    Min      1Q  Median      3Q     Max 
-1.2729 -0.7138  0.2853  0.7033  1.0711 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)
(Intercept)  5.469264  13.016791   0.420    0.681
C           -4.252429   5.135058  -0.828    0.423
I            3.120395   2.035671   1.533    0.149
Cr           0.002879   0.005764   0.499    0.626

Residual standard error: 0.9325 on 13 degrees of freedom
Multiple R-squared:  0.9235,    Adjusted R-squared:  0.9058 
F-statistic:  52.3 on 3 and 13 DF,  p-value: 1.629e-07

detach(datos1) # quito las variables de la memoria

Como se puede observar, ningún p-valor de la inferencia individual del modelo (0.681, 0.423, 0.149 y 0.626) es menor que 0.05. Por tanto, al nivel de significación del 5%, no se rechazaría la hipótesis de que los coeficientes del consumo, ingreso y crédito pendiente son cero.

Por otro lado, el p-valor asociado al contraste de significación conjunta (0.0000001629), sí es menor que 0.05. Por tanto, se rechaza la hipótesis de que todos los coeficientes de las variables independientes (excluido el término constante) son cero de forma simultánea.

Es decir, por un lado se tiene que ningún coeficiente es distinto de cero y, por otro, se estaría estableciendo que, al menos, hay uno distinto de cero. ¿Qué está pasando?

Cuando se tiene contradicción entre los contrastes de significación individual y conjunta, se ha de pensar que en el modelo analizado hay un problema de multicolinealdiad preocupante ya que esta infla las varianzas estimadas de los coeficientes estimados del modelo (y, por extensión, afecta a los contrastes de significación individual).

Inciso

Si en lugar de usar el p-valor, se optara por usar la región de rechazo, habría que comparar la columna referente al t value (en valor absoluto) con el valor teórico (en este caso de una t de Student con n-k = 17-4 = 13 grados de libertad). En todos los casos se observa que el valor experimental es inferior al teórico, por lo que no se rechaza la hipótesis nula:

texp = c(0.42, -0.828, 1.533, 0.499)
tteo = qt(0.975, 13) # help(qt)
tteo

[1] 2.160369

abs(texp) > tteo

[1] FALSE FALSE FALSE FALSE

De forma análoga, habría que comparar el valor dado en F-statistic (que es el experimental) con el valor teórico (en este caso de una F de Snedecor con k-1 = 4-1 = 3 y n-k = 17-4 = 13 grados de libertad). Se observa que el valor experimental es mayor que el teórico, por lo que se rechaza la hipótesis nula:

Fexp = 52.3
Fteo = qf(0.95, 3, 13) # help(qf)
Fteo

[1] 3.410534

Fexp > Fteo

[1] TRUE

Como no puede ser de otra forma, se llegan a las mismas conclusiones que usando el p-valor.

Relaciones espúreas a partir de la inferencia individual del modelo

Consideremos el conjunto de datos de Wooldridge sobre tipos de interés a 3, 6 y 12 meses:

datos2 = read.table("Wooldridge.txt", header=T, sep=";")
names(datos2) # r3 = tipos de interés a 3 meses, r6 = tipos de interés a 6 meses, r12 = tipos de interés a 12 meses

[1] "r3"  "r6"  "r12"

Si se plantea la regresión lineal simple en la que se analizan los tipos de interés a 12 meses en función de los tipos de interés a 3 meses, \(\textbf{r12} = \alpha_{1} + \alpha_{2} \textbf{r3} + \textbf{v}\), se obtienen los siguientes resultados:

attach(datos2) # agrego las variables a la memoria para poder usarlas por su nombre
modelo2 = lm(r12~r3)
summary(modelo2)

Call:
lm(formula = r12 ~ r3)

Residuals:
     Min       1Q   Median       3Q      Max 
-1.60881 -0.30527  0.00765  0.25587  1.95033 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  0.44040    0.09556   4.609 1.01e-05 ***
r3           1.00569    0.01343  74.905  < 2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.45 on 122 degrees of freedom
Multiple R-squared:  0.9787,    Adjusted R-squared:  0.9785 
F-statistic:  5611 on 1 and 122 DF,  p-value: < 2.2e-16

Se puede observar que la estimación obtenida es impecable desde un punto de vista técnico: coeficientes de las variables significativamente distintos de cero, modelo válido conjuntamente y coeficiente de determinación altísimo.

La interpretación de la estimación del coeficiente \(\alpha_{2}\) sería: cuando los tipos de interés a 3 meses aumentan un 1%, los tipos de interés a 12 meses también aumentan un 1%.

Si se añaden como variable independiente los tipos de interés a 6 meses, \(\textbf{r12} = \alpha_{1} + \alpha_{2} \textbf{r3} + \alpha_{3} \textbf{r6} + \textbf{v}\), la estimación por MCO proporciona los siguientes resultados:

modelo3 = lm(r12~r3+r6)
summary(modelo3)

Call:
lm(formula = r12 ~ r3 + r6)

Residuals:
     Min       1Q   Median       3Q      Max 
-0.82384 -0.08099 -0.01523  0.10864  0.41690 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  0.22471    0.03970   5.659 1.04e-07 ***
r3          -0.62891    0.06582  -9.555  < 2e-16 ***
r6           1.59334    0.06394  24.919  < 2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.1825 on 121 degrees of freedom
Multiple R-squared:  0.9965,    Adjusted R-squared:  0.9965 
F-statistic: 1.737e+04 on 2 and 121 DF,  p-value: < 2.2e-16

Se tiene de nuevo un análisis impecable desde un punto de vista técnico: coeficientes de las variables significativamente distintos de cero, modelo válido conjuntamente y coeficiente de determinación altísimo. Ahora bien, la interpretación de la estimación del coeficiente \(\alpha_{2}\) ahora sería: cuando los tipos de interés a 3 meses aumentan un 1%, los tipos de interés a 12 meses disminuyen un 0.62%.

¿Cómo es posible que usando los mismos datos se lleguen a conclusiones totalmente opuestas dependiendo del modelo planteado?

Observemos la representación gráfica de las tres variables:

plot(ts(datos2, start=1), plot.type="single", col=c("blue", "red", "orange"), ylab="Tipos de interés", xlab="Tiempo")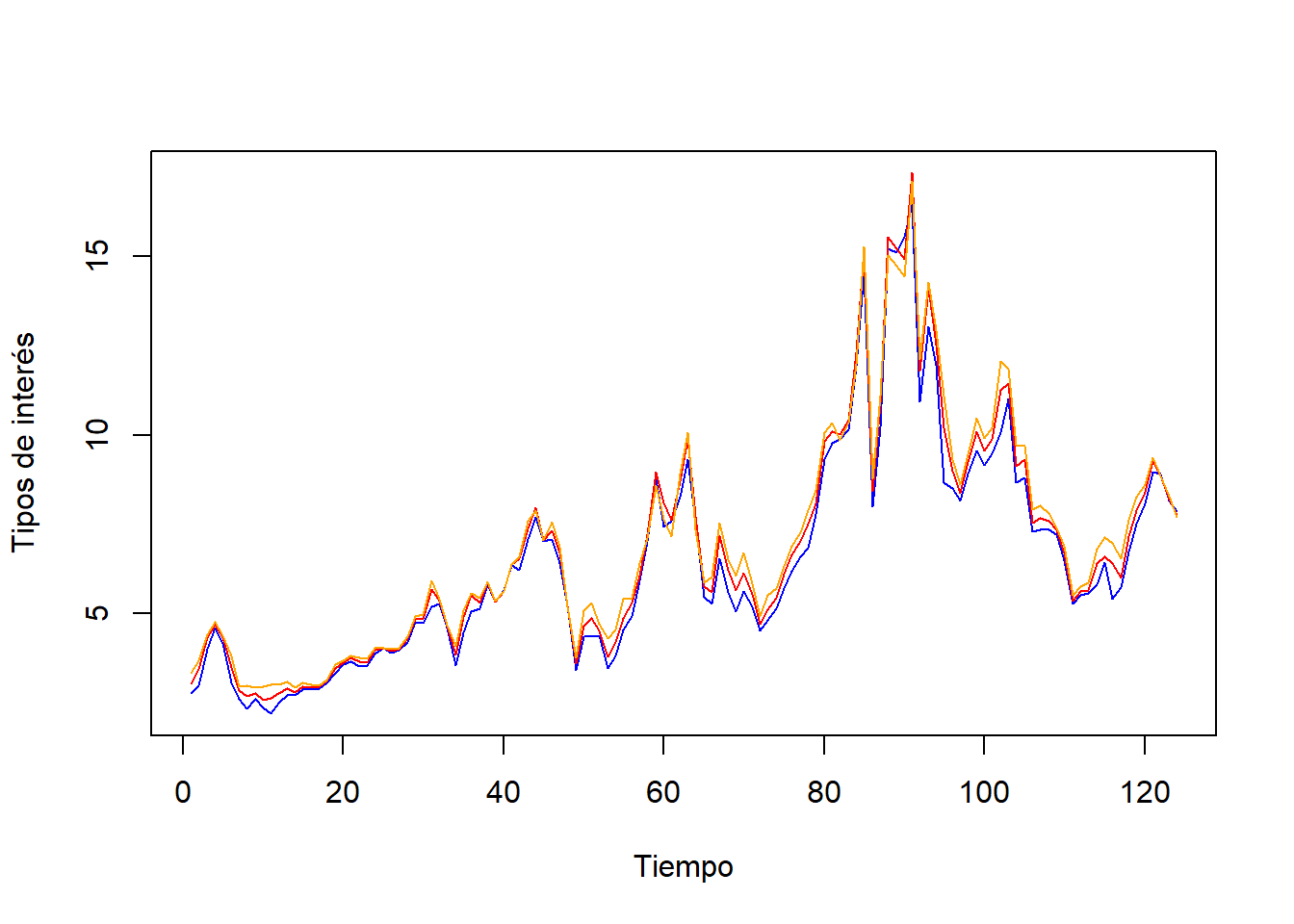

Se observa que prácticamente se solapan las tres, ¿cómo es posible decir que cuando los tipos de interés a 3 meses aumentan los tipos de interés a 12 meses disminuyen?

Si finalmente calculamos las correlaciones simples entre las tres variables:

cor(datos2)

           r3        r6       r12
r3  1.0000000 0.9965734 0.9893021
r6  0.9965734 1.0000000 0.9969508
r12 0.9893021 0.9969508 1.0000000

detach(datos2) # quito las variables de la memoria

Tenemos que la correlación entre los tipos de interés a 3 y 12 meses es prácticamente uno, 0.9893021, lo cual era esperable tal visualizar los datos. Este valor sugiere una alta relación lineal directa (cuando una aumenta, la otra también) entre ambas variables. Este resultado estaría en consonancia con los resultados obtenidos a partir del segundo modelo y en contradicción de los obtenidos a partir del tercero.

Y… ¿cuál es la diferencia entre el segundo y tecer modelo? Ni más ni menos que la inclusión de los tipo de interés a 6 meses y, resulta que los tipos de interés a 3 y 6 meses, están altamente relacionados linealmente (se tiene un coeficiente de correlación lineal simple muy próximo a uno, 0.9965734).

Cuando se obtienen coeficientes estimados no esperados, puede ser que éstos se deban a la alta relación lineal existente entre las variables independientes.

¡Ojo!

Los síntomas que aquí se muestran son pistas que deben hacernos pensar que pueda existir un problema de multicolinealidad preocupante, pero sólo eso. No son pruebas concluyentes que permitan determinar de forma inequívoca que se está ante un problema de multicolinealidad preocupante.

Por ejemplo, ¿por qué en el segundo ejemplo no se presenta la misma contradicción del primero si cuando calculamos las correlaciones del primero se obtienen que son similares a las del segundo?

attach(datos1) # agrego las variables a la memoria para poder usarlas por su nombre
  cor(datos1)

           D         C         I        Cr
D  1.0000000 0.9537283 0.9587877 0.9516305
C  0.9537283 1.0000000 0.9980960 0.9971663
I  0.9587877 0.9980960 1.0000000 0.9940621
Cr 0.9516305 0.9971663 0.9940621 1.0000000

detach(datos1) # quito las variables de la memoria

Referencias

• Wissel, J. (2009). A new biased estimator for multivariate regression models with highly collinear variables. Ph.D. thesis.
• Wooldridge, J.M. (2000). Introductory Econometrics: A modern approach. South-Western, Cegage Learning.