casos = c(2, 2, 2, 2, 3, 9, 17, 33, 54, 81, 135, 192, 263, 341, 532, 755, 1078, 1511, 2275, 3256,
4402, 5873, 7593, 8185, 8299, 8468, 8634, 8805, 8932, 9116, 9176, 9238, 9328, 9466, 9719,
11448, 13936, 17633, 21672, 26161, 31674, 36551, 41176, 48822, 54071, 57368, 66309, 75467,
83727, 90133, 95934, 97407, 103993, 104072, 111499, 119047, 126283, 132956, 138526, 142169,
147438, 153010, 158732, 163334, 167941, 171897, 175057, 178260, 182759)
t = length(casos)
dia = 1:tSi dentro del post dedicado a la Estadística Descriptiva Bidimensional se abordaba la recta de regresión, a continuación se va a profundizar en este análisis, haciendo especial hincapié en situaciones donde la relación lineal es mejorable.
Para ellos vamos a considerar el número de casos positivos de COVID19 observados a primeros de marzo del año 2020 junto a una componente temporal que hace referencia al día en el que se registra dicho número de positivos:
Modelo lineal simple
En primer lugar, consideraremos la posibilidad en la que el número de casos es explicado a partir de la tendencia: \[\textbf{casos} = a + b \cdot \textbf{dia} + \textbf{u}\]
reg1 = lm(casos~dia)
summary(reg1)
Call:
lm(formula = casos ~ dia)
Residuals:
Min 1Q Median 3Q Max
-42064 -23528 403 22546 43586
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -46350.3 6387.6 -7.256 5.26e-10 ***
dia 2766.2 158.6 17.439 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 26240 on 67 degrees of freedom
Multiple R-squared: 0.8195, Adjusted R-squared: 0.8168
F-statistic: 304.1 on 1 and 67 DF, p-value: < 2.2e-16Si bien el análisis de los resultados nos dice que estamos ante un modelo válido, si se representan los datos observados y la recta estimada, podríamos pensar que la estimación realizada es mejorable ya que la relación no es muy lineal que se diga:
plot(dia, casos, type="b", col="blue", xlab="Día", ylab="Número de CASOS", main="Casos detectados COVID19 en España", lwd=3)
abline(reg1, col="red", lwd=3)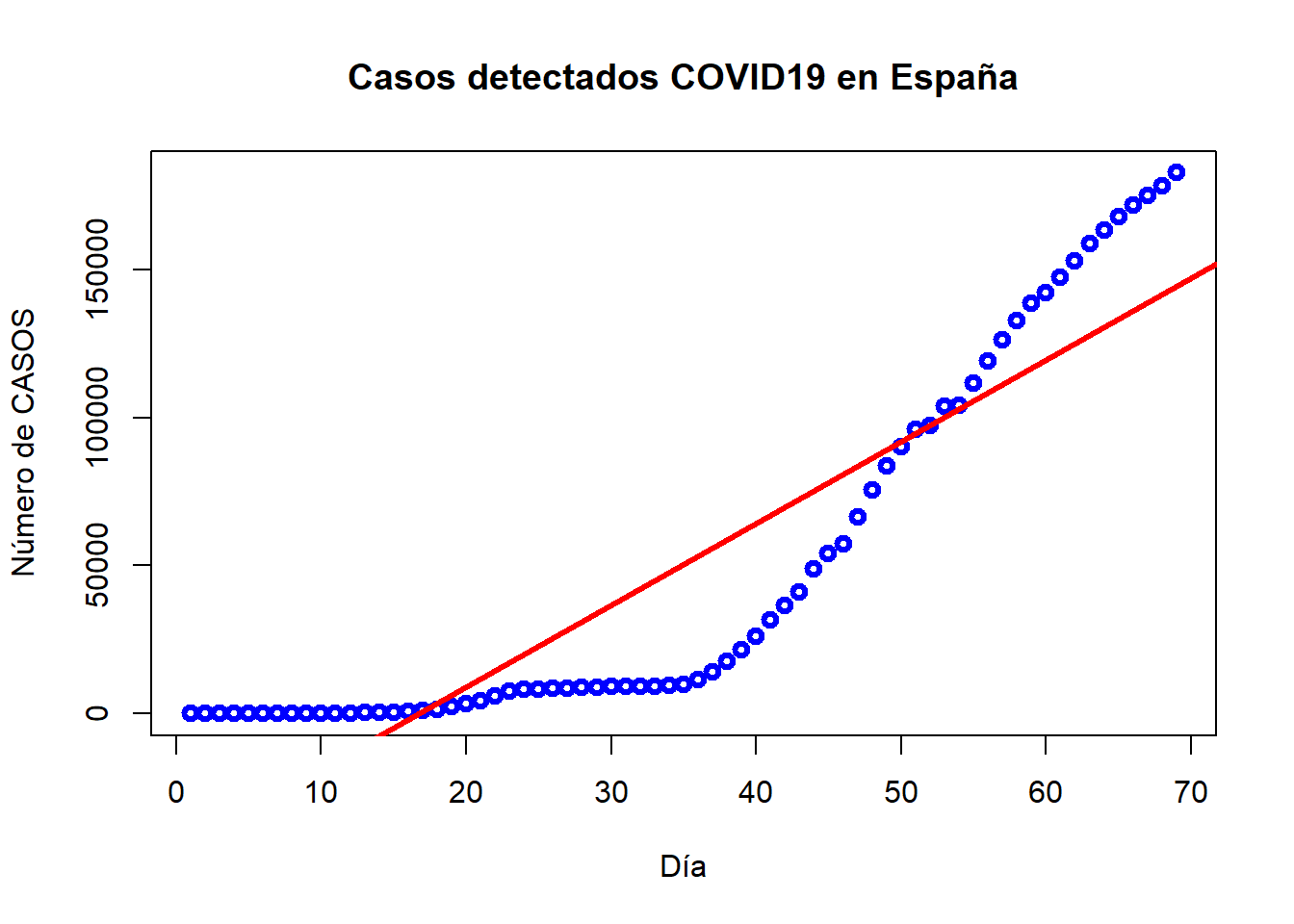
Modelo doblemente logarítmico
Una primera posibilidad es plantear el modelo potencial: \[\textbf{casos} = a \cdot \textbf{dia}^b \cdot exp(\textbf{u})\]
Dicho modelo no es lineal, pero puede linealizarse fácilmente tomando logaritmos: \[log(\textbf{casos}) = A + b*log(\textbf{dia}) + \textbf{u}\] donde \(A = log(a)\).
La estimación de \(b\) se obtendría directamente, sin embargo, para la de \(a\) habría que deshacer la transformación logarítmica hecha: \(a = exp(A)\).
En este caso, la estimación de este modelo vendría dada por:
log.casos = log(casos)
log.dia = log(dia)
reg2 = lm(log.casos~log.dia)
summary(reg2)
Call:
lm(formula = log.casos ~ log.dia)
Residuals:
Min 1Q Median 3Q Max
-1.6178 -0.2918 0.0767 0.2437 3.7912
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -3.0981 0.3121 -9.926 8.65e-15 ***
log.dia 3.6127 0.0918 39.356 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.6881 on 67 degrees of freedom
Multiple R-squared: 0.9585, Adjusted R-squared: 0.9579
F-statistic: 1549 on 1 and 67 DF, p-value: < 2.2e-16Se tiene que \(a = e^{-3.0981} = 0.04513488\) y \(b = 3.6127\).
Igualmente se tiene un modelo válido, en el que se ha producido un aumento considerable en el coeficiente de determinación. ¡Ojo! Cuidado con este comentario, ya que realmente estoy comparando modelos donde la variable dependiente es distinta, por lo que el aumento del coeficiente de determinación se podría deber a un aumento de la suma de cuadrados totales y no a una disminución de la suma de cuadrados de los residuos.
En cualquier caso, al representar el logaritmo de los casos positivos y la recta ajustada, se observa un mejor comportamiento que en el caso lineal:
plot(log.dia, log.casos, type="b", col="blue", xlab="Día", ylab="Número de CASOS (escala logarítmica)", main="Casos detectados COVID19 en España", lwd=3)
abline(reg2, col="red", lwd=3)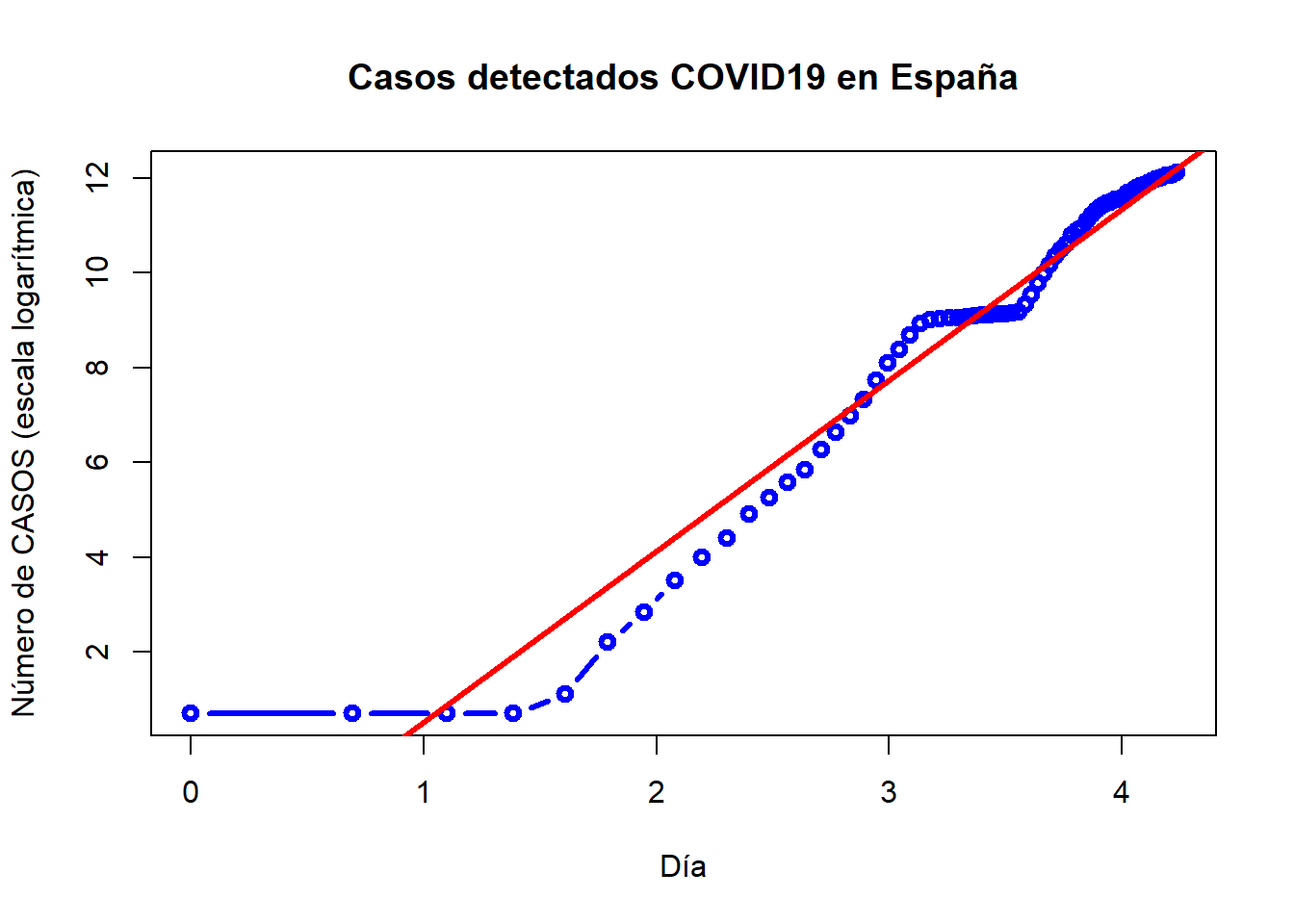
Esta sensación se confirma representando los valores observados en la variable dependiente y estimados a partir del modelo:
series2 = ts(cbind(casos, exp(reg2$fitted.values)), start = 1)
plot(series2, plot.type="single", type="b", col=c("blue","red"), lwd=3, ylab="Número de CASOS", xlab="Día", main="Casos detectados COVID19 en España y estimación")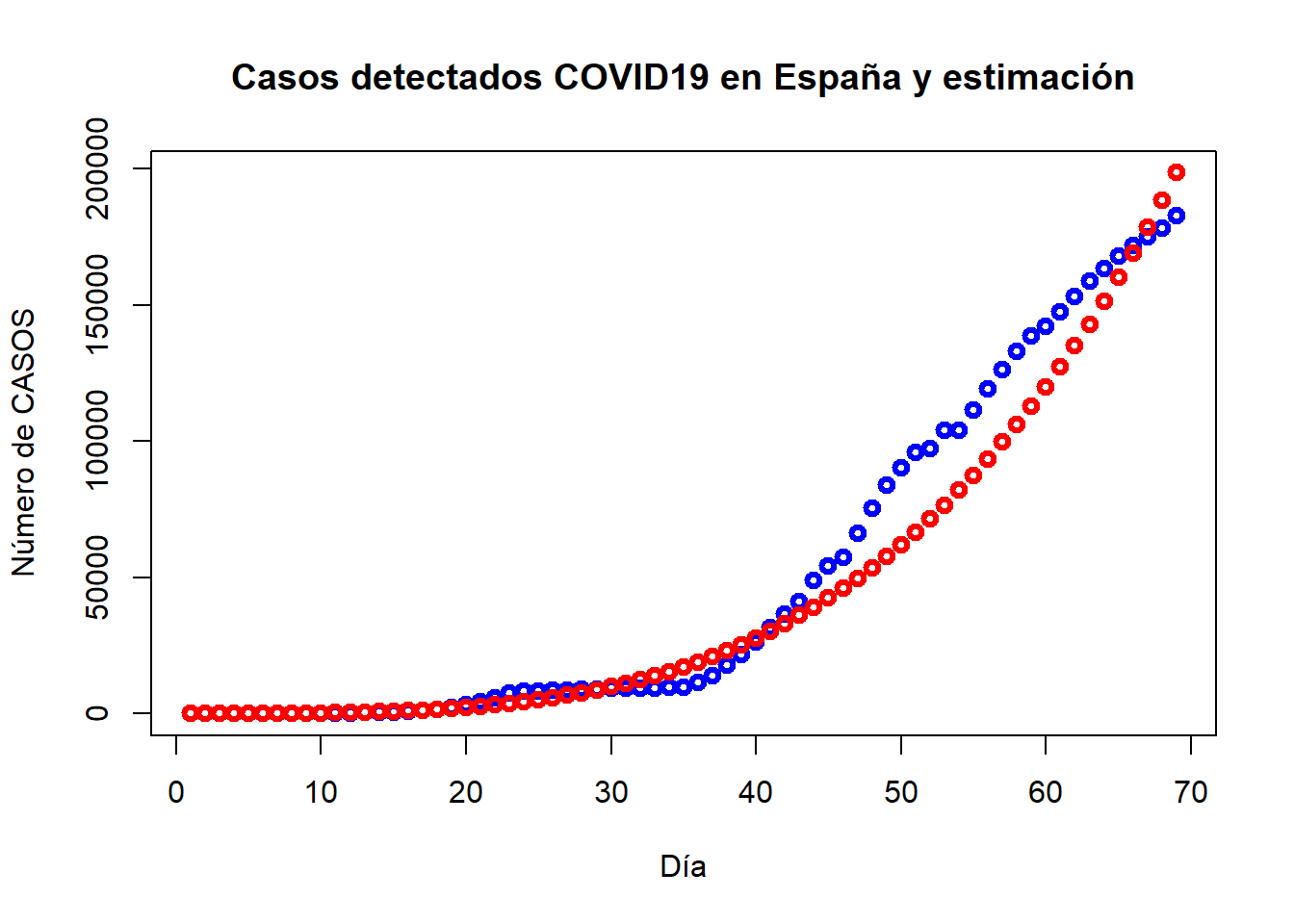
¡Ojo! Mediante la opción reg2$fitted.values se obtienen los valores estimados del modelo, es decir, de \(log(\textbf{casos})\). Por tanto, para recuperar la estimación de los datos originales hay que deshacer la transformación logarítmica realizado mediante la exponencial.
Modelo log-lineal
otra opción es plantear el modelo exponencial: \[\textbf{casos} = exp(a + b \cdot \textbf{dia} + \textbf{u})\]
Una vez más, dicho modelo no es lineal pero puede linealizarse fácilmente tomando logaritmos: \[log(\textbf{casos}) = a + b \cdot \textbf{dia} + \textbf{u}\]
En este caso, la estimación de los parámetros \(a\) y \(b\) se obtendría directamente mediante:
reg3 = lm(log.casos~dia)
summary(reg3)
Call:
lm(formula = log.casos ~ dia)
Residuals:
Min 1Q Median 3Q Max
-3.2873 -0.7599 0.4369 0.7033 2.0344
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 3.365706 0.323827 10.39 1.31e-15 ***
dia 0.153691 0.008041 19.11 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 1.33 on 67 degrees of freedom
Multiple R-squared: 0.845, Adjusted R-squared: 0.8427
F-statistic: 365.3 on 1 and 67 DF, p-value: < 2.2e-16Se tiene un peor ajuste en términos del coeficiente de eterminación que en el modelo anterior (adviértase que ambos modelos tienen la misma variable dependiente, por lo que son comparables).
La representación del ajuste realizado se obtiene mediante el siguiente código:
plot(dia, log.casos, type="b", col="blue", xlab="Día", ylab="Número de CASOS (escala logarítmica)", main="Casos detectados COVID19 en España", lwd=3)
abline(reg3, col="red", lwd=3)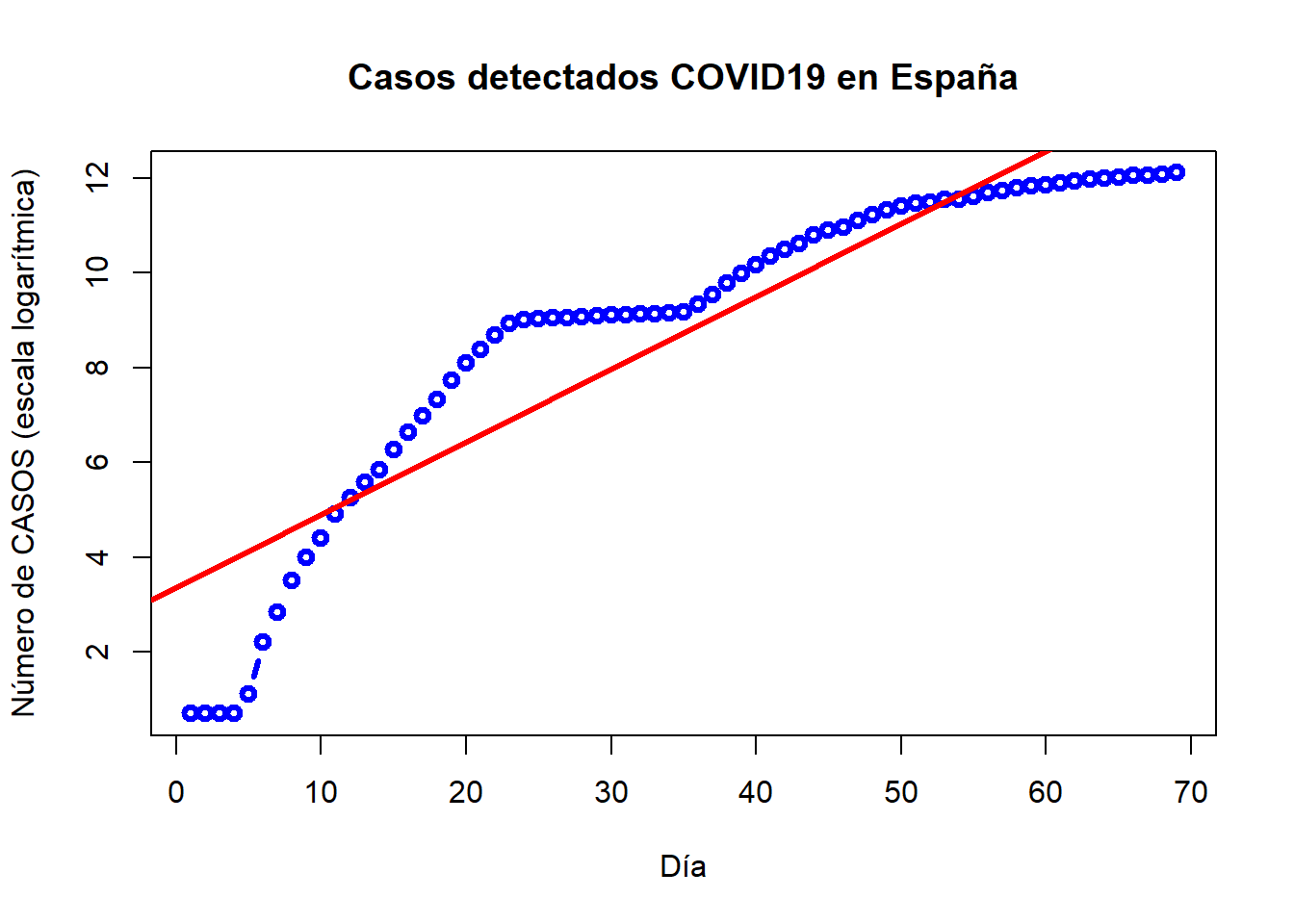
Mientras que la representación conjunta de los valores estimados y observados es la siguiente:
series2 = ts(cbind(casos, exp(reg3$fitted.values)), start = 1)
plot(series2, plot.type="single", type="b", col=c("blue","red"), lwd=3, ylab="Número de CASOS", xlab="Día", main="Casos detectados COVID19 en España y estimación")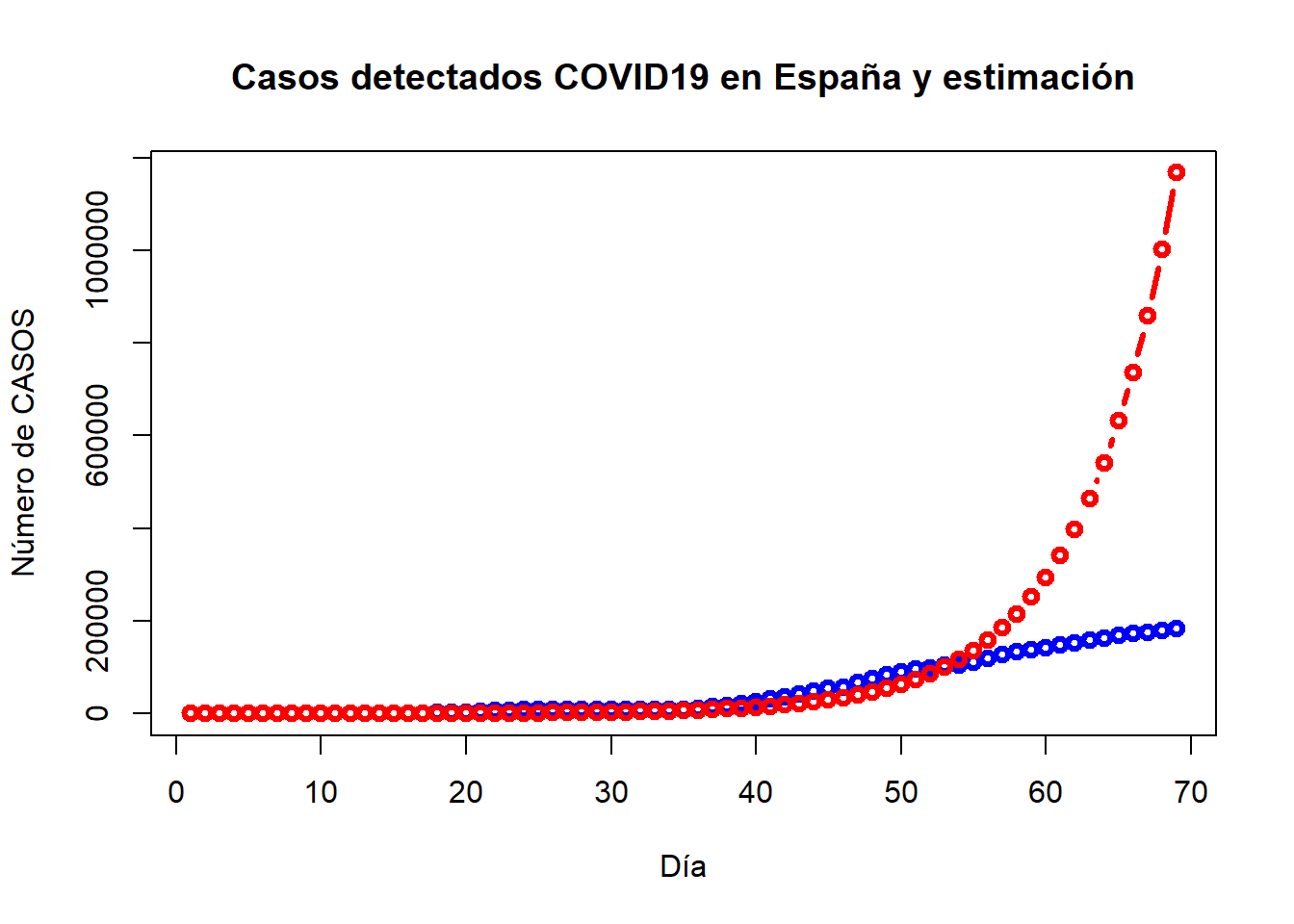
Se observa que falla clamorosamente en los últimos casos (el crecimiento no es exponencial en la información que se tiene).
Selección del modelo
Aunque se tiene a estas alturas más o menos claro el modelo más adecuado, no sobra realizar una comparación final:
# install.packages("memisc")
library(memisc)Loading required package: latticeLoading required package: MASS
Attaching package: 'memisc'The following objects are masked from 'package:stats':
contr.sum, contr.treatment, contrastsThe following object is masked from 'package:base':
as.array mtable(reg1, reg2, reg3)
Calls:
reg1: lm(formula = casos ~ dia)
reg2: lm(formula = log.casos ~ log.dia)
reg3: lm(formula = log.casos ~ dia)
====================================================
reg1 reg2 reg3
------------- --------- ---------
casos log.casos log.casos
----------------------------------------------------
(Intercept) -46350.257*** -3.098*** 3.366***
(6387.599) (0.312) (0.324)
dia 2766.214*** 0.154***
(158.620) (0.008)
log.dia 3.613***
(0.092)
----------------------------------------------------
R-squared 0.819 0.959 0.845
N 69 69 69
====================================================
Significance: *** = p < 0.001; ** = p < 0.01;
* = p < 0.05 Una vez descartado el primer modelo por no tener una relación lineal en los datos, que los otros dos modelos tengan la misma variable dependiente me permite seleccionar aquel con un mayor coeficiente de determinación. Por tanto, en este caso sería preferible un modelo doblemente logarítmico.